Kepler's Law of Equal Areas states the radius of a planet's orbit (as drawn between itself and the Sun) will cover equal areas of space in equal amounts of time.
Depending on where the planet is in its orbit, its radius and its angular velocity is subject to change due to the gravitational pull between it and the Sun.
The planet will travel at a higher velocity as it approaches the Sun, causing it to cover more distance over time, and it will travel more slowly when it is farther away from the Sun, causing it to cover less distance over time.
In the time dt, the planet clears a triangle having the base r and height r dƟ with an area dA=1/2 * r *rd(Ɵ).
From this, the constant areal velocity can be written as dA/dt=1/2 r^2 dƟ/dt.
The area enclosed by the elliptical orbit is πab.
So the period (P) works with P * 1/2 r^2 dƟ/dt = πab.
The average motion of the planet as it orbits the Sun is n= 2π/P and it works with r^2 dƟ= abn dt.
Fowler, Michael. "Deriving Kepler’s Laws from the Inverse-Square Law." Galileo. University of Virginia, n.d. Web. 22 Apr. 2015. <http://galileo.phys.virginia.edu/classes/152.mf1i.spring02/KeplersLaws.htm>.
"Kepler's Laws of Planetary Motion." Wikipedia. Wikimedia Foundation, n.d. Web. 22 Apr. 2015. <http://en.wikipedia.org/wiki/Kepler's_laws_of_planetary_motion#The_inverse_square_law>.
Newton’s Proof of Kepler’s Second Law (n.d.): 1-2. Department of Mathematics. University of Kansas. Web. 22 Apr. 2015. <http://www.math.ku.edu/~lerner/m500f09/NewtonKepler.pdf>.
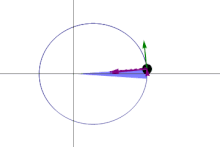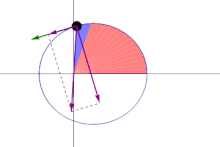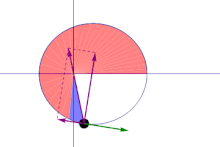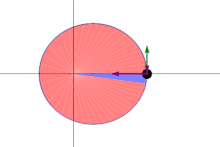 |
| The blue section maintains the same area. |
Depending on where the planet is in its orbit, its radius and its angular velocity is subject to change due to the gravitational pull between it and the Sun.
The planet will travel at a higher velocity as it approaches the Sun, causing it to cover more distance over time, and it will travel more slowly when it is farther away from the Sun, causing it to cover less distance over time.
In the time dt, the planet clears a triangle having the base r and height r dƟ with an area dA=1/2 * r *rd(Ɵ).
From this, the constant areal velocity can be written as dA/dt=1/2 r^2 dƟ/dt.
The area enclosed by the elliptical orbit is πab.
So the period (P) works with P * 1/2 r^2 dƟ/dt = πab.
The average motion of the planet as it orbits the Sun is n= 2π/P and it works with r^2 dƟ= abn dt.
Fowler, Michael. "Deriving Kepler’s Laws from the Inverse-Square Law." Galileo. University of Virginia, n.d. Web. 22 Apr. 2015. <http://galileo.phys.virginia.edu/classes/152.mf1i.spring02/KeplersLaws.htm>.
"Kepler's Laws of Planetary Motion." Wikipedia. Wikimedia Foundation, n.d. Web. 22 Apr. 2015. <http://en.wikipedia.org/wiki/Kepler's_laws_of_planetary_motion#The_inverse_square_law>.
Newton’s Proof of Kepler’s Second Law (n.d.): 1-2. Department of Mathematics. University of Kansas. Web. 22 Apr. 2015. <http://www.math.ku.edu/~lerner/m500f09/NewtonKepler.pdf>.
No comments:
Post a Comment