Kepler's Third Law

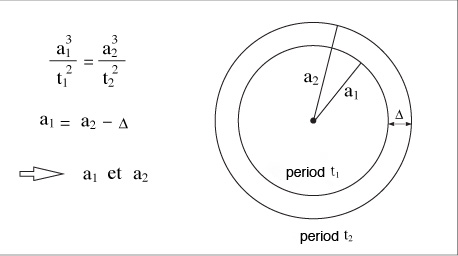
The third law, the Law of Harmonies, relates the period of a planet's orbit, T, to the length of its average radius. It states that the square of the period of the orbit T is proportional to the cube of the radius r, and that every planet around the same Sun has the same constant of proportionality.


The proof begins with dA/dt = l/(2 m), the expression to represent the area swept out by the radius of the planet's orbit.
Multiply both sides by dt to get dA = [l/(2 m)] dt.
This can be integrated to get an expression relating the total area of the orbit to the period of the orbit:
A = [l/(2 m)] T.
Square both sides and solve for T^2:
T^2 = 4 (m2/l2) A^2.

The area A of an ellipse is pi a b, where a is the length of the semimajor axis and b the length of the semiminor axis. Thus our expression of T^2 becomes:
T^2 = 4 pi^2 (m2/l2) a^2 b^2.

b is related to a and c, the distance between the focus and the center, by a2 = b2 + c2, 

so b^2 = a^2 - c^2: T2 = 4 pi^2 (m^2/l^2) a^2 (a^2 - c^2).

Since c = a e, we find that
T^2 = 4 pi^2 (m^2/l^2) a^2 (a^2 - a^2 e^2)
T^2 = 4 pi^2 (m^2/l^2) a^2 [a^2 (1 - e^2)]
T^2 = 4 pi^2 (m^2/l^2) a^4 (1 - e^2).

Then, a property of ellipse geometry is used which indicates that e p = a (1 - e2).

Factor out a (1 - e^2) from our expression of T^2 and replace it with e p .

T^2 = 4 pi^2 (m^2/l^2) a^3 [a (1 - e^2)]
T^2 = 4 pi^2 (m^2/l^2) a^3 (e p).

T2 is proportional to a3. Kepler's first law shows that e p = l2/(G m2 M). Substitute this into our expression for T^2 to find that T^2 = 4 pi^2 (m^2/l^2) l^2/(G m^2 M) a^3. The m2 and l2 cancel, and we are left with T^2 = (4 pi^2)/(GM) a^3. (4 pi^2)/(GM) is the constant of proportionality. It depends on G (which represents the universal constant of gravitational force) and M, the mass of the sun around which the planets orbit. As a result, the square of the period of a planet is proportional to the cube of the length of the semimajor axis (radius), and this rule applies to all planets and satellites with complete elliptical orbits.

The above proof is adapted from:

"Francis, Erik M. "Kepler's Laws: Kepler's Third Law." Kepler's Laws: Kepler's Third Law. Alcyone Systems, 2015. Web. 22 Apr. 2015. <http://www.alcyone.com/max/physics/kepler/6.html>."

"The Apple, the Moon, and the Inverse Square Law." The Physics Classroom. N.p., n.d. Web. 22 Apr. 2015. <http://www.physicsclassroom.com/class/circles/Lesson-3/The-Apple,-the-Moon,-and-the-Inverse-Square-Law>.