Supporting Calculus Concepts

Kepler's laws, as defined by calculus, can be explained with the help of certain advanced concepts. Different methods of proving the laws involve different types of steps. Some of the supporting concepts are briefly explained below.

Cross Products  A cross product is the resultant vector from two vectors crossed with one another. It is orthogonal from the other two vectors, meaning that it lies on the plane perpendicular from the plane of the two factor vectors. Go here to find more information on how to find cross products.

Angular momentum 
The angular momentum of a object in orbit (mass=m) with respect to a chosen origin is given by
 L = mvr sin θ . Angular momentum is the linear velocity of a point on a circle, and it is represented by a vector tangential to the edge of the circle.

Unit vectors These are special vectors that have a magnitude of one and no units (like the radius of a unit circle). To symbolize a unit vector, mathematicians typically use a lowercase letter and top them with a circumflex. For instance, ĵ is a j with a circumflex, and it is pronounced "j-hat."
Unit vectors come in handy when multiplying; for instance, a scalar (an amount given that has magnitude but no direction) multiplied by a unit vector will take on the direction (angle) of the vector but keep its magnitude. Therefore, if the vector ĵ of 55° is multiplied by 7 m/s, then the product becomes 7 m/s at a direction of 55° from the x-axis.

Polar coordinates  Cartesian coordinates is what the average math student learns to use first. This involves a point system with x- and y-coordinates. But polar systems are a bit different: rather than using the x-and-y coordinates to locate a point on a graph, higher-level calculus problems, especially those involving celestial orbits, tend to use the point's angle from the horizontal, or x-axis (remember the unit circle?) and its distance from the origin. Think of the point as being on the edge of a circle, and its distance from the origin being the radius. To convert Cartesian coordinates to polar coordinates, you can use the x- and y-coordinates as legs of a right triangle, and solve for the angle on the origin using trigonometry. An example is given below:




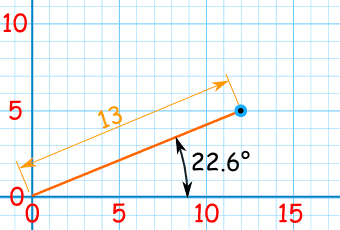
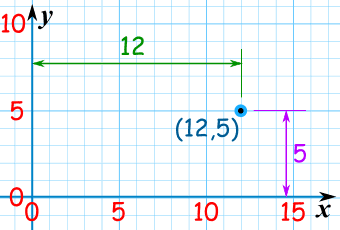
Partial differentiation Partial differentiation is involved in proving Kepler's second law. It involves differentiating an equation with multiple variables (both x and y are in the main equation). For more information on how to solve a partial derivative, click here.

Calculus symbol reference See an equation and don't understand what you're looking at? This handy list of calculus symbols might help you decode the message. If at first you don't succeed, try, try again.



"Polar and Cartesian Coordinates." Math Is Fun. Math Is Fun, 2014. Web. 22 Apr. 2015. <https://www.mathsisfun.com/polar-cartesian-coordinates.html>.